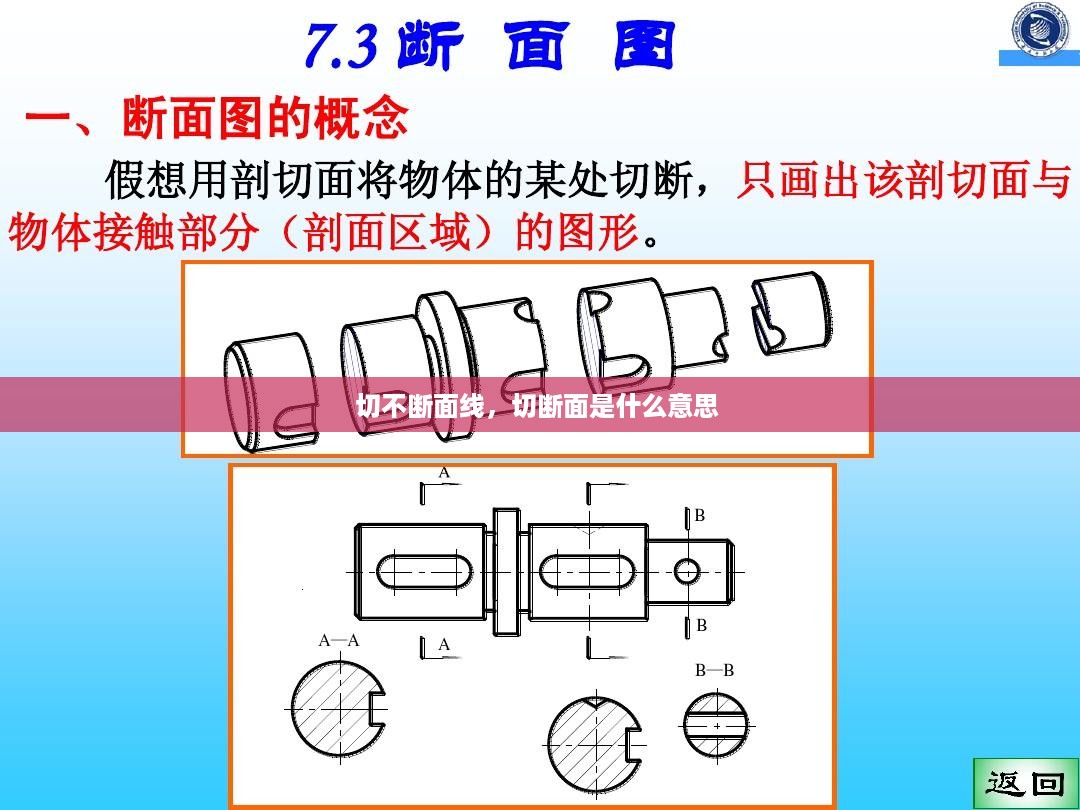
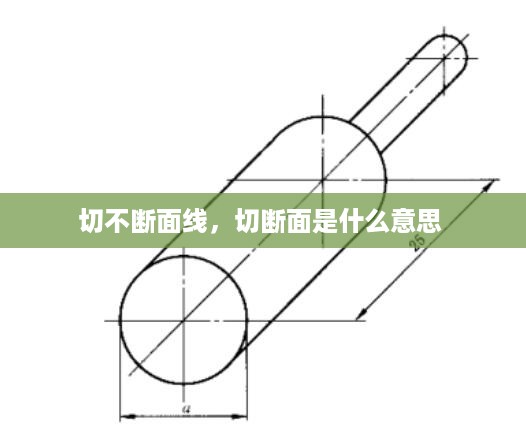
什么是切不断面线

切不断面线，也被称为不可切割线，是指在几何学中，某些特定的几何图形中存在的一种特殊线段。这种线段具有独特的性质，即无论在何种角度或位置进行切割，都无法将其完全分离或断开。切不断面线在数学和工程学等领域有着广泛的应用。

切不断面线的几何性质

切不断面线通常出现在一些特定的几何图形中，如正多边形、圆形等。以下是一些切不断面线的几何性质：

• 在正多边形中，切不断面线可以通过将正多边形的对角线连接起来形成。例如，正五边形的切不断面线就是通过连接相邻顶点和相对顶点形成的线段。

• 在圆形中，切不断面线可以是圆的直径，因为无论从哪个角度切割圆形，直径都无法被完全切断。

• 在某些特殊的几何图形中，切不断面线可以是两条相交的线段，它们在任何角度切割下都无法完全分离。

切不断面线的数学原理

切不断面线的存在与数学中的对称性原理密切相关。以下是一些解释切不断面线数学原理的要点：

• 对称性：切不断面线往往出现在具有高度对称性的几何图形中。对称性使得线段在任何角度切割下都保持不变，从而无法被切断。

• 角度关系：在某些情况下，切不断面线的存在与几何图形的角度关系有关。例如，正多边形的切不断面线与内角和外角的关系密切相关。

• 欧几里得几何：切不断面线的原理也适用于欧几里得几何中的各种图形。欧几里得几何的公理和定理为切不断面线的存在提供了数学基础。

切不断面线的实际应用

切不断面线不仅在理论数学中有着重要的地位，而且在实际应用中也具有重要意义。以下是一些切不断面线在实际中的应用实例：

• 建筑设计：在建筑设计中，切不断面线的原理可以帮助设计师避免在结构设计中出现不可切割的线段，从而确保建筑的安全性。

• 材料科学：在材料科学中，切不断面线的原理可以帮助研究人员理解材料的微观结构，从而设计出具有特定性能的材料。

• 工程学：在工程学中，切不断面线的原理可以应用于机械设计、电路设计等领域，以确保设计的合理性和可靠性。

  

切不断面线的挑战与探索

尽管切不断面线在数学和实际应用中具有重要意义，但对其深入理解和探索仍然存在一些挑战：

• 非欧几里得几何：在非欧几里得几何中，切不断面线的性质可能会有所不同，这为数学家提供了新的研究方向。

• 复杂图形：对于复杂图形中的切不断面线，其存在性和性质的研究可能会更加困难，需要新的数学工具和方法。

• 跨学科研究：切不断面线的研究可以促进数学与其他学科的交叉，为解决实际问题提供新的思路。

结论

切不断面线是几何学中一个独特的概念，它不仅具有丰富的数学内涵，而且在实际应用中也具有重要意义。通过对切不断面线的深入研究，我们可以更好地理解几何学的原理，并将其应用于解决实际问题。随着数学和科技的不断发展，切不断面线的研究将会继续深入，为人类社会的发展做出更大的贡献。